In 1996, I submitted my Ph.D thesis on so-called dynamic scale-space theories for solving human and computer vision problems. These problems range from stereo and color vision by the human brain to robust scene analysis and categorization by robots or the detection and identification of tumor tissues in medical images.
Over the last 25 years besides working throughout Europe on related but quite mundane issues in domains like air pollution or smart grids I kept quite intrigued in finding a solution to what I would call instantaneous renormalization of such theories.
What do I mean with this? Instead of starting off from a very local perspective on e.g. signal and image analysis I was looking for ways to connect the local to the global of such signals or images and vice versa, not only for now but forever. Of course, this is not new. In the past I also worked like many others on e.g. geometric shortening flows on surfaces of 3D objects trying to keep the surface area constant during the transformation from scale to scale. Scale transformation here refers to the powers of ten idea in which you zoom in or out on the earth and see more or less detail. But in this case the whole process is defined intrinsically by the object under study - not to say indeed the same happens when we simply look around. The difficulty in human or artificial vision and many other related areas like robotics (where control forms the other side of the coin of artificial intelligent systems) is to make operational all those details and connections and their dynamics at once.
In this blog I provide a glimpse of how this can be achieved by building so-called generalized master equations working on jet bundles and their geometric and topological properties living above one-dimensional nonlinear non-stationary signals, drown in either additive or multiplicative noise - I know you will complain about all those concepts but I beg you to buy me time to elaborate on that. Below you find an original input signal which looks like a sinusoidal which it is certainly not followed by one with additive and multiplicative noise added, respectively. Next, the final result of applying such a master equation that captures both local (a-) symmetries as well as all non-local aspects and conservation laws throughout the re-normalization process.
In forthcoming blogs, I will devote more time on the theory behind these new insights acquired over the last 5 years in Mr. NeC. I will also point out many areas of applications besides for general AI for this forgotten Killer Science of more than a century back.
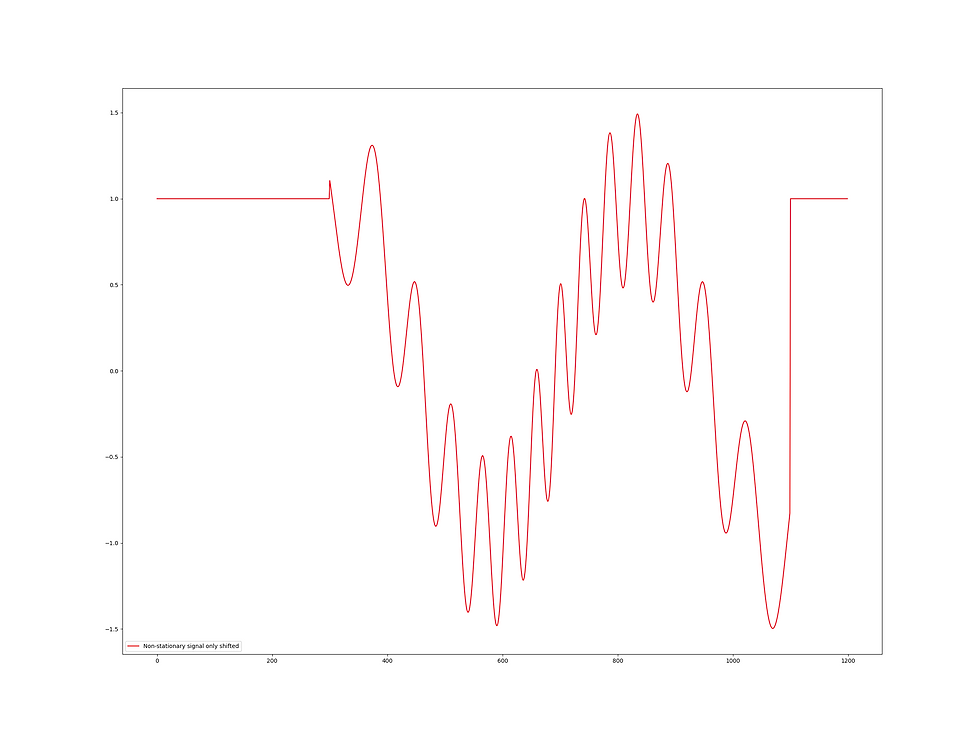
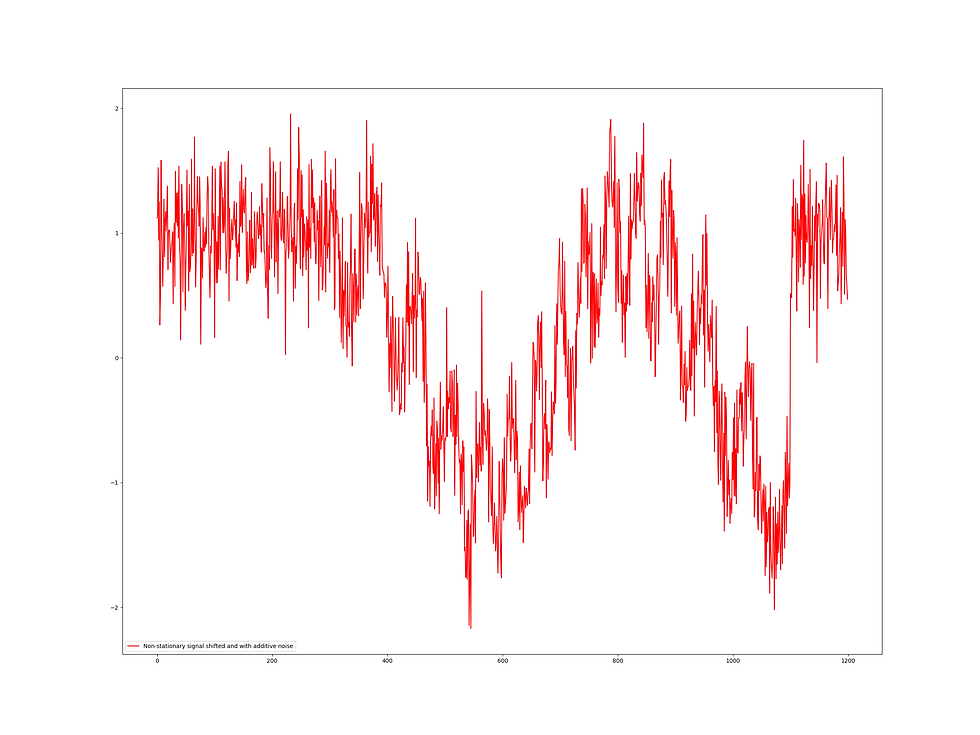
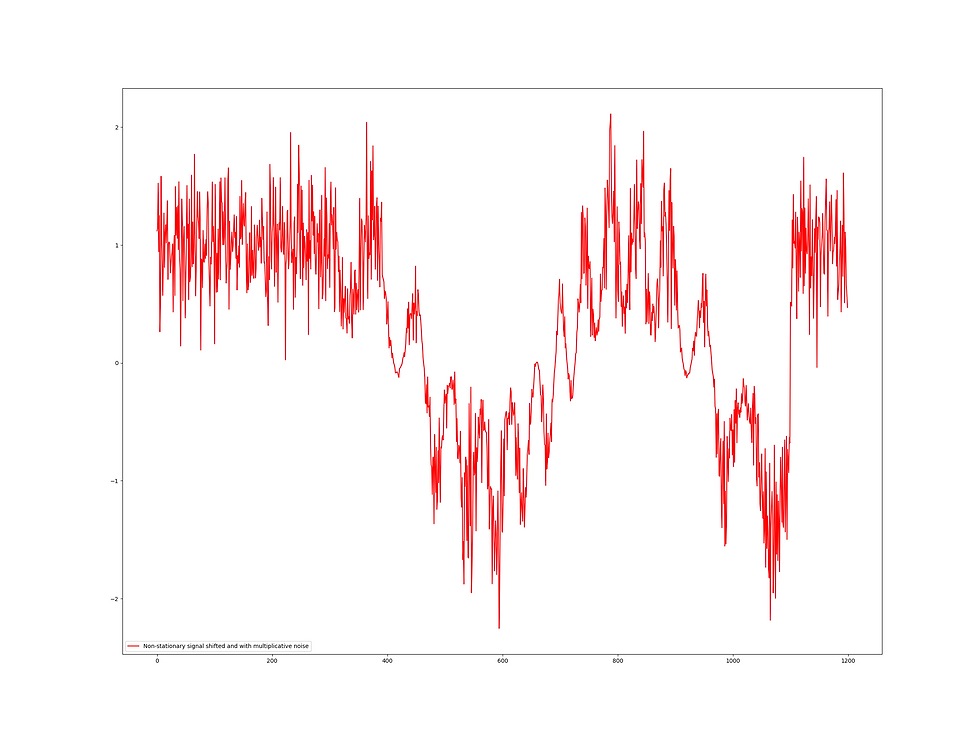
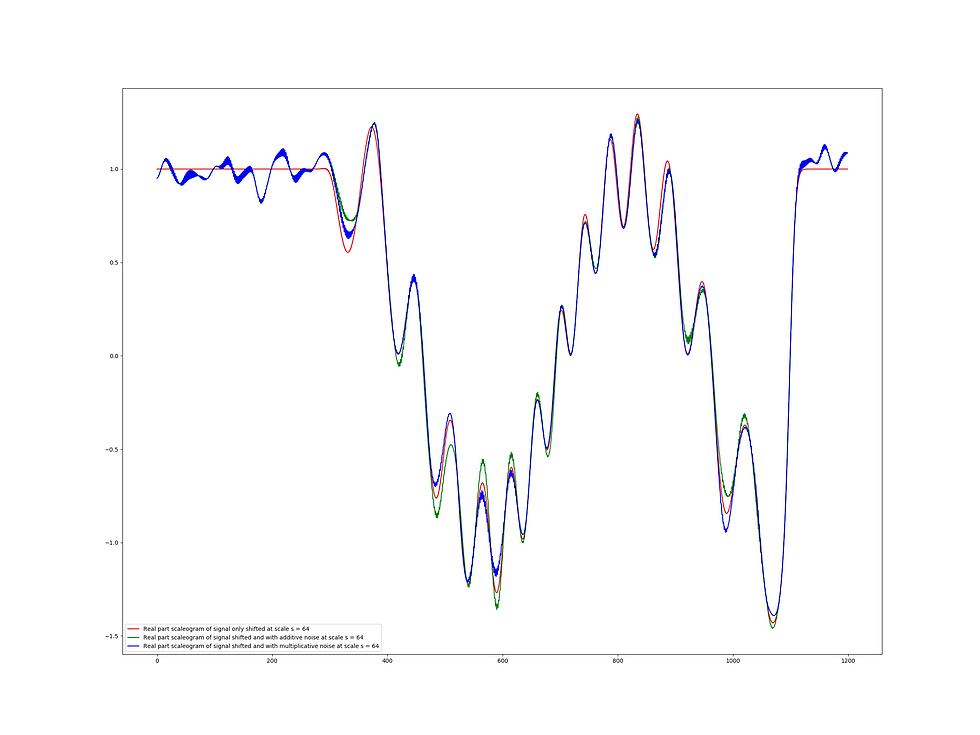
To raise your appetite and start background reading: re-normalized dynamic scaling does away with empirical and extended dynamic mode decomposition ... and Koopman operator learning.


Comentarios